Yet another solution to a very simple exercise.

Problem

One of the exercises proposed in the third chapter of The Algorithm Design Manual¹ is this one:

3-4. Design a stack S that supports S.push(x), S.pop(), and S.findmin(), which returns the minimum element of S. All operations should run in constant time.

Right now it seems that the website of the book doesn’t provide a solution (most likely because it is a pretty simple one).

Anyway, this exercise is also provided by LeetCode.

Some solutions

An obvious path to follow to solve this problem is to create a stack and to use an external variable to handle the minimum value, taking care to update it after every push(x) and most of all after every pop(x). Yet, this leaves us with a new issue: if the pop(x) interests that minimum value, how do we track the previous minimum value, so that we can serve it when getMin() is called?

I realised most people do like this: they create a second stack; when pushing a new value they insert whatever is smallest between the one they are inserting and the last minimum value recorded.

For instance this is the code that this brilliant youtube channel proposes:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class MinStack:

    def __init__(self):
        self.stack = []
        self.minStack = []

    def push(self, val: int) -> None:
        self.stack.append(val)
        val = min(val, self.minStack[-1] if self.minStack else val)
        self.minStack.append(val)

    def pop(self) -> None:
        self.stack.pop()
        self.minStack.pop()

    def top(self) -> int:
        return self.stack[-1]

    def getMin(self) -> int:
        return self.minStack[-1]

Oh yes, it works and it does so even in time complexity $\mathcal{O}(1)$, as requested in the assignment!

Other similar approaches exist in the Discussion section of LeetCode².

Issues with these approaches

The above method carries a burden: the size of the second stack grows linearly with the length of the main one, doubling the memory usage.

Another way

We still create the two stacks.

At the start, both of them are empty: during the first push(x) we add the same value to both stacks.

During the following push(x) calls we will be more careful: we always add the value to self.stack, nonetheless in the stack tracking the minimum values (in my code that’s self.minS) we save only the val if it is smaller or equal to the last element contained in self.minS.

When we pop()³ a value from the main stack (self.stack) we delete it from self.minS only if the val popped is the same as the last value saved in self.minS.

By operating in this way we are guaranteed that self.minS saves the minimum values in decrescent mode, being always certain to work in $\mathcal{O}(1)$ without duplicating (in the average case and when the stack grows) our memory footprint.

This is the naïve implementation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

class MinStack:

    def __init__(self):
        self.stack = []
        self.minS = []

    def push(self, val: int) -> None:

        # Initially both stacks are empty
        if not self.stack:
            self.stack.append(val)
            self.minS.append(val)
        else:
            if val <= self.minS[-1]:
                self.minS.append(val)
            self.stack.append(val)
                
    def pop(self) -> None:
        popped = self.stack.pop()
        
        # We delete the last only if it is
        # equal to the minimum value
        if popped == self.minS[-1]: 
            del self.minS[-1]

    def top(self) -> int:
        return self.stack[-1]

    def getMin(self) -> int:
        return self.minS[-1]

Comparing the two approaches

In order to see how the different approaches behave with larger values of n, the following set of instructions have been fed through the cProfile python module.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

def run():
    obj = MinStack()
    attempts = 1_000_000
    min_len, stack_len = 0, 0
    for i in range(attempts):
        x = random.randint(-100, 100)
        obj.push(x)
        obj.top()
        obj.getMin()
        min_len += len(obj.minStack) # or obj.minS
        stack_len += len(obj.stack) 

        # we want to pop less often, to highlight the 
        # differences (when push(x) and pop() aren't simmetrical)
        if x % 2 == 0:
            obj.pop()
    print(f"Avg length of obj.minStack: {min_len/attempts}")
    print(f"Avg length of obj.minS:     {stack_len/attempts}")

To be noted that:

• as a random int is inserted during the loop, results will vary slightly;
• min_len and stack_len are incremented before pop() on purpose;
• we want the size of the stack to grow (pop() must happen less frequently than push(x)), otherwise it’s granted that both stacks will always have the same length.

Before

The first solution explored above generates the following result:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

Avg length of obj.minStack: 249034.230154
Avg length of obj.minS:     249034.230154
         17781331 function calls in 5.594 seconds

   Ordered by: standard name

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
  1000000    0.661    0.000    1.045    0.000 005-a.py:10(push)
   502392    0.224    0.000    0.309    0.000 005-a.py:15(pop)
  1000000    0.122    0.000    0.122    0.000 005-a.py:19(top)
  1000000    0.118    0.000    0.118    0.000 005-a.py:22(getMin)
        1    1.595    1.595    5.587    5.587 005-a.py:25(run)

    # Omitting irrelevant functions here

Of course with the first method the two stacks have always the same length. The whole function took 5.59 seconds.

When submitted to LeetCode it returned:

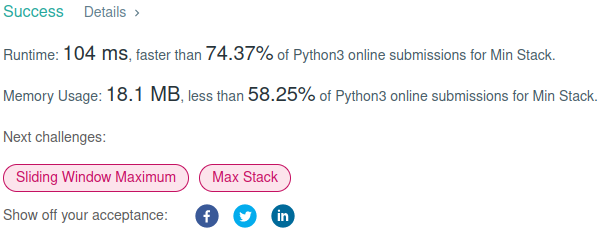
After

Let’s do the same for our script and explore the size of the stacks as we did before:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

Avg length of obj.minS:     2497.844128
Avg length of obj.minS:     249004.41381
         15287241 function calls in 4.740 seconds

   Ordered by: standard name

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
  1000000    0.363    0.000    0.454    0.000 005-b.py:10(push)
   502262    0.174    0.000    0.218    0.000 005-b.py:21(pop)
  1000000    0.118    0.000    0.118    0.000 005-b.py:29(top)
  1000000    0.114    0.000    0.114    0.000 005-b.py:32(getMin)

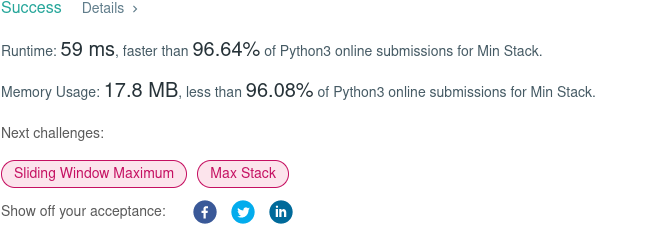
I’m not that impressed by the improvement, albeit minor, in speed (a marginal 4.74 seconds), but by the reduction (two orders of magnitude⁴) in the average length of self.minS!

At submission, even LeetCode noticed the improvement⁵.

_{Last version: 8365627B0DCFEDF1B17B77EB4F33EB6C99ABB1BD26BF4FA7CDB57F9FAB1E6BA6.}